Author:
Attila Kiss was born in Budapest, in 1967. He went to an agricultural secondary school in Vác and then he turned into another direction and continued his studies in Pázmány Péter Catholic University. He runs a horse-riding school in Csömör currently and he is the leader of the Zengő Nyíl Archery School. He researches, reconstructs and tests bows from the Migration Period. He has been publishing the data that he is harvesting from his studies. He is also an author, he writes books of youth literature.

Translator:
Rita Somogyi was born in Budapest, in 1976. After finishing secondary school, she went to the Teacher Training Faculty of Károli Gáspár Calvinist University, then Juhász Gyula Teacher Training College and lastly, obtained Master Degree of Teaching in Szeged University. For 26 years, she has been teaching English. She started doing archery in 2007 and took part in several competitions in Hungary and abroad. She won the Hungarian National Championship in 2016, and became second in the European Championship in the same year. She shoots modern material traditional bows.

„THEIR BOW LIKE GOD’S ARM, NO ESCAPE FROM THEIR ARROWS”
The examination of the Use Value of Steppe-type Horn-Tendon Bows and Arrows

Attila Kiss

The composite bows, made from horn, wood and sinew, are still covered by the mist of mystery in the “traditional” archery network in our country. According to misbeliefs, these bows shoot unbelievably far, they simply cannot be drawn, according to others, their lifespan is only 1-2 years. However, they all agree on their being priceless.
In the school of The Hungarian Historical Archery Society (Magyar Történelmi Íjász Társaság), under the supervision of experienced bowyers, those who have some manual skills can make their own composite bows. Throughout the years, the Association, arm-in-arm with archaeologists, took enormous steps to get to know the frightening weapon of our nomadic ancestors. The Zengő Nyíl Historical Equestrian and Archery Organisation (Zengő Nyíl Történelmi Lovas és Íjász Egyesület) represents the historical branch of mounted archery, its horsemen try to model the erstwhile military situations, and they have been using horn-sinew bows exclusively in their re-enactments.
As a result of the fertile cooperation of the organisation and the bowyers on the field of reconstructing and using the Steppe-type composite bows and the historical arrows, I was looking for answers for the emerging questions in my experiment. During it, I tested three different horn-sinew composite bows (Scythian, Settlement era[1] Hungarian and Ottoman) with different constructions and build from several historical ages, from the aspect of their real values in battlefields. Furthermore, I also examined the efficacy of arrows with different weights, materials and tips used in various historical ages.
When measuring the operational values of the three bows, I don’t want to draw any historical inference, the data and conclusions only relate to these three bows and the structure of each. My tests are parts of a sequence of experiments, whose antecedents can be found in others’ researches and tests both abroad and in Hungary. Gábor Szőllősy had already elaborated the mechanics of several bow types thoroughly in his doctoral dissertation[2] and it provided great help to me.
As a first step in November 2018, on the archery range of the Zengő Nyíl Historical Equestrian and Archery Organisation we shot all the arrows with all three bows, we measured their initial velocity, averaged them, then we evaluated their performance in distance shooting, then tested the penetration of the arrows on ballistic gel, which is considered to be homogenous in my opinion, then on shields made of 2.3 cm thick pine boards, finally we shot all arrows on a lamellar leather and felt armour, which was rather for curiosity but less measurable. We shot with thumb release by using a thumb ring.
In November 2019, I involved two more bows in the experiment, then in March and April 2020, I put one of the arrowheads to newer tests.
Throughout the experiment, I got help and advice from Gábor Szőllősy as well as Murat Özveri, leader of Tirendaz archery club in Istanbul, who himself had also experimented with different bows and shooting techniques several times. In the latter part of the experiment, Gábor Szőllősy helped me with his advice and calculations. The shots were executed by Murat Özveri, as well as Róbert Kovács and Csaba Greskó who are the archers of the Zengő Nyíl Historical Equestrian and Archery Organisation and by me. The pictures were taken by my son, Levente Kiss, the detailed photos and videos were taken by Nelli Kőmíves, a student of the organisation. She also made the digital version of the diagrams and charts. I would like to thank all of them.

Description of the bows tested during the experiment

Our first bow was a Scythian type bow, which according to Holger Riesch’s description can be considered to be the reconstruction of the Subex bow.[3] The bow was found in grave 27 of the Subex burial-place, south-east from the oasis town of Turpan, in China, and is dated to V-III century BC. Its bowyer is Endre Kommendánt (Picture 1). The bow is composed of two-two bunch-berry (Cornus mas) wands that were laminated and glued together, and an Ox (Bubalus bubalus) horn-stripe placed and glued in between the pairs of wooden laminates (Picture 2).

Picture 1

Picture 2
The maker glued the constituents together with Red deer (Cervus elaphus) sinew-glue, then he glued Red deer horn plates on the belly (surface facing the archer) of the bow core. The plates start off from the centre of the bow but they don’t reach the reflexes.
The maker glued several layers of red deer sinew on the back (surface facing the target) of the bow. The notion of “layer” in this case means gluing the sinew at one stroke, dispersedly, almost filum by filum, by applying thin layers of it one by one. At this stage the bow is covered with red deer sinew winding from the tip of the lower reflex to the tip of the upper reflex.
The bow in unstrung state is not as prestressed[4] as a Turkish flight bow or a Korean bow, actually, it proves itself to be a string-follower[5]. Similarly to the Subex finding, the reconstruction is asymmetric, 128 cm long measured on its back side from tip to tip (the original one is 120 cm long)[6] (Pictures 3-4). An interesting part of it is its triangular cross-section on the limbs and grip, apart from the oval cross-section of the reflexes.

Picture 3

Picture 4

Unlike the steppe bows which we know, the Subex bow is the widest at its grip (3.4 cm) and the narrowest at the deflex[7] parts (2.2-2.3 cm), at the same time, it is the thickest here too, so the bow doesn’t bend at the deflex parts, but on the straight section of the limb and at the reflexes, which means that the functioning of the lever is completely different, and this way, the strained part of the bow is somewhere else than of the bows with rigid ears in general (Pictures 5-6).

Picture 5

Picture 6

This is the reason why the measuring parameters, used for bows with rigid ears, cannot be used for Scythian type bows. The angle, included by the two straight lines drawn from the two tips to the middle of the grip, is 140˚ and it is approximately in conformity with the grip angle of bows with rigid ears. Its brace height is 8 cm[8], string length is 115 cm, string material is dacron (16-strain) (for homogeneity, I tested all bows with dacron strings, although strings made of raw leather stripes work excellently).
Bow II of the experiment was made by me following the parameters given by The Hungarian Historical Archery Society. It can be considered to be a type-reconstruction, based on the shape and size of the antler plates at both sides of the rigid ears and of the grip, which were found in the graves where weapon-related burial customs are seen, in the supposedly Settlement era Hungarian burial-places from the 10th century in the Carpathian basin.[9]
The spine of the bow is composed of a 90 cm long ash (Fraxinus ornus) wood core, into which I glued the ash wood ears by dovetailing method using hide glue. I also used hide glue to glue the grip in the middle of the 160˚ bent wooden core (Pictures 7-9).

Picture 7

Picture 8

Picture 9

I put two ox horn plates on the belly of the bow, from the middle of the grip to the end of the wooden core; I glued 110 g of red deer sinew on the back in three layers. Then, I covered the back with catfish leather, and the belly wasn’t covered. (An interesting thing: a worm bit through the horn of the upper limb before gluing but it didn’t influence the functionality of the bow. Picture 10)

Picture 10

The grip and bow ear plates weren’t made of deer antler but horn. The unstrung bow from tip to tip, measured straight: 129 cm, the strung bow: 128 cm. String length: 117.5 cm, material: 16-strain dacron. The distance between the string nock and the tip is 4.62 cm. The ear is 2.55 cm thick at the root, 1.70 cm in the middle, 1.28 cm at the string nock. Ear angle: 28˚, grip angle: 166˚, limb length: 34 cm, ear length: 24.5 cm; limb width at its widest point: 3.7 cm, limb thickness in the middle of the bending part: 1.38 cm; bow weight: 586 g.
An Ottoman-Turkish bow was the next one, which I made based on the parameters of the bow-making school of the Hungarian Historical Archery Society given by Sándor Paku. The grip has a rhomboid shape made of ash wood. I glued the two 47 cm long ash wood limbs to the grip by dovetailing method using hide glue. The ears were also glued to the limbs by dovetailing method using hide glue. (Picture 11)

Picture 11

The ears are not bent but carved from ash wood. To avoid breaking due to the steep ear angle, I glued a horn plate/section into each ear.
Hungarian Grey Cattle (Bos primigenius taurus hungaricus) horn plates (cut from the horn of the animal) were put on the belly of the bow from the centre to the root of the ear.
I glued three layers of altogether 110 g red deer sinew on the back using hide glue. While gluing the sinew, I didn’t pull the bow ears too close together, unlike the Turkish flight/distance shooting bows’, therefore after stringing and using for the first time, the bow didn’t show the drastic ‘C’-shape when unstrung. (Pictures 12-14).

Picture 12

Picture 13

Picture 14

The back of the bow III wasn’t covered during the experiment. The unstrung bow from tip to tip, measured straight: 89.8 cm, the strung bow: 108.7 cm. Ear length: 9.5 cm. The distance between the string nock and the tip is 2.5 cm. The ear is 1.45 cm thick at the root, 1.52 cm in the middle, at the string nock: 1.48 cm. Ear angle: 75˚, limb length (with kasan gözü[10]): 44 cm; limb width at its widest point: 3.55 cm, limb thickness in the middle of the most intensely bending part: 1.62 cm. Grip angle: 149˚, brace height: 19.5 cm, string length: 103.5 cm, its material: dacron (16-strain). Bow weight: 438 g.

Picture 15

Experiments

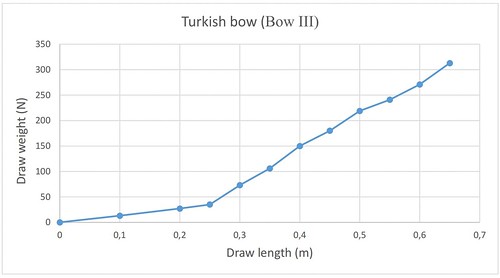
The poundage of a bow plays the biggest role in its usefulness, in other words, in its real battlefield utility value, however, this “efficacy” can be increased by increasing the grip angle[11], shortening the working limbs, increasing the ear angle and shortening the ears.[12] With these ideas, the poundage of the bow, its energy storing capacity and the initial velocity of the launched arrow can also be increased (Illustrations 1-4). The correlations seen in the illustrations were revealed by Gábor Szőllősy, therefore during my experiment I didn’t want to deal with the mechanics of the bows in detail.
Illustration 1 – 10˚ increase of the angle of the bow ears Illustration 2 – 5 cm shortening of the bow ears

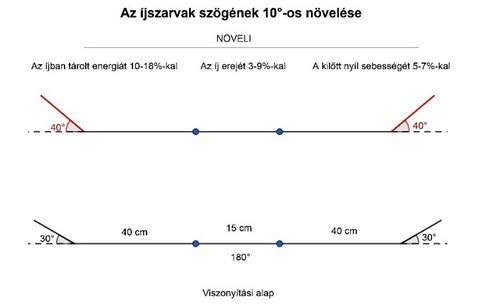
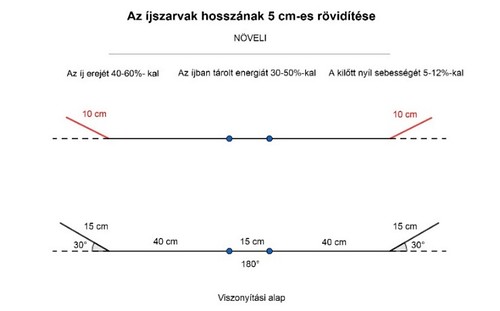
Illustration 3- 2.5 cm shortening of the flexible limbs of the bow

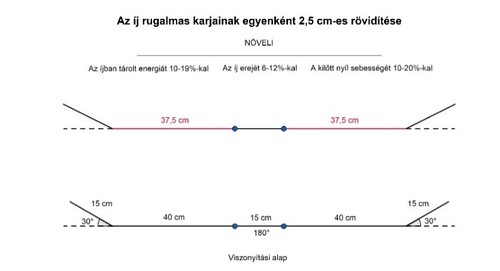
Illustration 4 – 10˚ reduce of the grip angle of the flexible bowlimbs

In the archery and bowyer society, many consider the degree of the grip reflex of the strung bow, in other words, the rate of the grip’s recurve, to be the standard grip angle. Not the angle which is included by the straight lines which connect the centreline of the two ear roots and the centre of the grip, but the angle included by the straight lines which connect the initial part of the limbs coming from the grip is considered as grip angle. (The latter one is the angle of the grip reflex of a strung bow, Pictures 16-17).

Picture 16

Picture 17

According to this measurement, the Scythian type bow has the steepest grip angle, so it should present the optimum values. According to the ear angle, the Hungarian and the Turkish bows should perform almost the same. And according to measuring the grip reflex angles, the Hungarian bow would stand on the second, the Turkish bow on the third place.
However, my measuring data showed another result. We measured the initial velocity of all arrows launched by all three bows with a CHRONY model 1 chronograph placed 2 metres from the bows. Apparently, the launched arrow, while moving away from the anchor point, loses some of its kinetic energy and this loss is directly proportional to the covered distance (until deadlock). Erhard Godehardt put the chronograph 1 m from the launching point[13], while Holger Riesch put it 50 cm[14] from it. (The data of different devices on different distances can be compared only after telling over, however, I elaborated only the data which was harvested from the chronograph on 2 m.)
I decided on a 65-cm draw length at all three bows, adapted to the draw length of the Scythian type bow. We shot the arrows using a shooting rack, however, due to the unusual grip shape of Bow I, it could not be able to mounted to the rack, so distance shots with the Scythian type bow were released by hand.
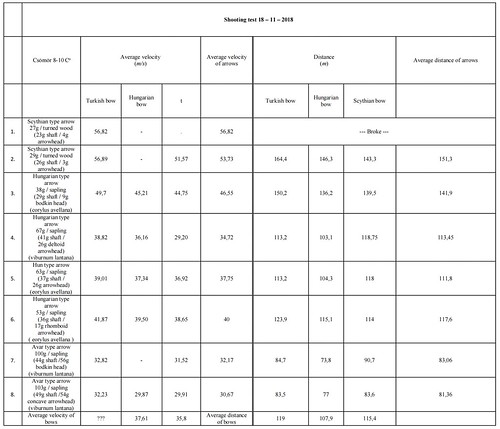
With the 65-cm draw length, the Scythian bow (I) produced 74 lb draw weight, the Hungarian bow (II) 55 and the Turkish bow (III) 65 lb draw weight. Considering the average of all the launched arrows, Bow I provided 35.8 m/s, Bow II 37.61 m/s, Bow III 40.32 m/s initial velocity.
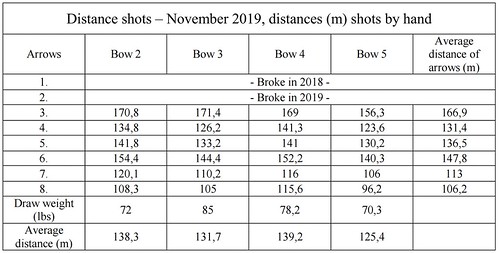
At distance shooting, with 65-cm draw length, considering the average of all the launched arrows, Bow I produced 115.4 m, Bow II 107.9 m and Bow III 119 m. The maximum shot range of Bow I was 143.3 m, of Bow II was 146.3 m and of Bow III was 164.4 m. Unfortunately, the shooting rack was not suitable for adjusting in a 45-degree angle, so we repeated the distance shots manually with Bow II and Bow III. The average of the shots and the maximum distance was the biggest in the case of Bow II (Appendix 3).
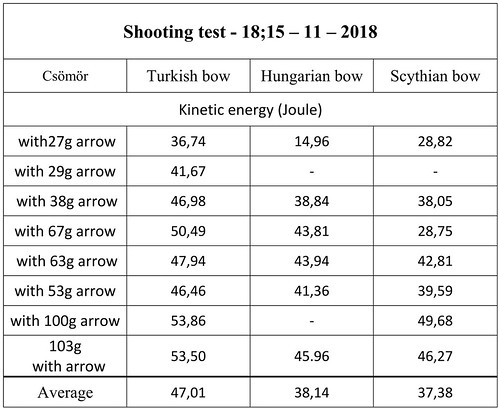
The kinetic energy of Bow I was 37.38 Joule on average, of Bow II was 38.14 Joule and of Bow III was 47.01 Joule. (The kinetic energy, calculated using Arrow 4 (67 g, short cutting edge, deltoid tip), was 35 Joule by Bow I, 44 Joule by Bow II and 82 Joule by Bow III.) After studying all the given data above and the appendix thoroughly, we can see that despite the big draw weight, the Scythian type bow didn’t present those values which I was expecting considering the initial velocity of the arrows, the kinetic energy and the distance shots.
I adapted the 65-cm draw length to the constraints of Bow I, but the ideal draw length of the other two bows by their structure is not 65 cm.
Finally, I identified the ideal draw length of Bow II and Bow III during distance shooting by hand. Bow II produced 65 lb, Bow III 83 lb power on 70-cm draw length. Then we drew Bow II till 75 cm, here it produced 77 lb power.
We launched the distance shots with 70 lb draw weight with Bow II, and with 80 lb draw weight with Bow III. After meticulous measurement, I marked the ideal draw length, which produces the given draw weight, on each arrow. This way, the average of the shots of Bow II was 146.5 m, and 131 m with Bow III. The maximum distance (reached with the ideal arrow) was 176 m with Bow II, and 174.5 m with Bow III. To my surprise, Bow II with its 10 lb lower draw weight presented a 15.5 m higher average.
While evaluating the data, another astonishing fact emerged: the K-value (Klopsteg-value) was 40.6 g at Bow I, only 39 g at Bow II and 67.6 g with Bow III. The K-value is a part of the potential energy which is needed to move the limbs and indicates the arrow mass (in gram) that could be shot using this part of potential energy[15]. From the aspect of the real value in use, a lower K-value is more beneficial because a bigger part of potential energy is used for driving the arrow and a smaller part for driving the bow itself which is a “wasted” energy from the point of view of the arrow. In the regard, the Hungarian bow achieved best.
The shape of an unstrung bow is determined by both the ear and the grip angle, also by the negative bending of the limbs, the so-called prestressed state. When the bowyer glues the sinew-layers on the back of the bow, he pulls the ears of the bow closer to each other gradually towards the back. After gluing the third layer, the ears almost touch each other into negative direction. A bow like this is not easy to string. However, if the bowyer pulls the bowlimbs less towards each other, the bow will have a slighter C-shape. A bow made this way is easier to string. In other words: the potential energy of the bow is directly proportional to the square of its shape change, as well as to the mathematical constant defining its flexibility. For example, if a bow that is straight in unstrung position and a C-shape prestressed bow have the same flexibility constant, their potential energy depends on the rate of (elastic) deformation. The C-shape bow is getting more ‘elastically’ deformed during stringing, so after stringing its potential energy will be higher. In a simpler way: it is easier to string a straight bow or a bow which is bent towards the stringing direction in unstrung position (deflex), so it demands less energy from the person who strings it, than a bow which has to be bent through a longer way from the opposite direction. Obviously, the stringing person puts more energy into the strung bow when bending it back from the opposite direction. (So the energy used for shooting an arrow is composed of the potential energy of the prestressed bow and the additional potential energy stored in the very same limbs when the bow is drawn.)
It can explain why Bow I (the Scythian type bow) presented lower values than the other two, despite its relatively high draw weight. The bowyer didn’t pull Bow I together towards the back when gluing the sinew, therefore the shape of the unstrung bow hardly differentiates from the shape of the strung bow, this way, the potential energy is lower (Picture 18).

Picture 18

Bow I is the reconstruction of the Subex bow. It was found in a burial-place which is similar to those of Pazyryk culture, and probably it was put into the grave in strung state. In all depictions that I know, the bow is depicted in strung state (Pictures 19-22).[16]

Picture 19

Picture 20

Picture 21

Picture 22

So we don’t know the shape of the unstrung and “rested” Scythian bow. The bowyers consider the shape of the strung bow as a basis, so they make the unstrung bow similar, which doesn’t store as much energy as a negative C-shaped unstrung bow. However, if the Scythian bow had a C-shape in unstrung state (Picture 23), presumably its values would be better than of Bow I (used in the experiment). I couldn’t test the bow in the picture due to the limits of the experiment (Pictures 24-26).

Picture 23

Picture 24

Picture 25

Picture 26

Beside the unfavourable unstrung shape of Bow I, in my opinion, another reason for the “sluggishness” and “stacking” on 65 cm can also be the fact that it is composed of 4 wands and a horn stripe glued between them. I would be able to prove my opinion if I made the twin of Bow I as for the shape but with a different structure and measured the same way as Bow I. This could be the next step of the reconstruction of the Scythian type bow.

Bows involved in experiments in 2019

Bow IV was made by Vilmos Pári (The Hungarian Historical Archery Society) and it is a Hungarian type bow form the 10th century. It is made of ash wood (Fraxinus ornus), ox horn and deer sinew, covered with birch bark (Betula Pendula) (Pictures 27-28).

Picture 27

Picture 28

Its length from tip to tip, measured straight in unstrung state: 103.4 cm, strung state: 132 cm, string length: 119 cm, material: dacron (16-strain). Distance between string nock and tip:4.9 cm. Ear thickness at root: 2.92 cm, in the middle: 1.65 cm, at string nock: 1.15 cm. Ear length: 24.5 cm, ear angle: 59˚. Grip angle: 153˚, limb length: 33 cm, limb width at widest point: 4.18 cm, limb thickness in the middle of bending part: 1.08 cm, brace height: 17.3 cm, with shorter string: 21.5 cm. Weight: 689 g, grip size: 2.62×3.55 cm. Grip plates and lateral ear plates are made of red deer (Cervus elaphus) antler.
Bow V is an Ottoman Turkish style bow made by Vilmos Pári (Pictures 29-30).

Picture 29

Picture 30

Its length from tip to tip, measured straight in unstrung state: 108 cm, strung state: 116 cm. String length: 109 cm, dacron (16-strain). Distance between string nock and tip: 2.65 cm. Ear thickness at root: 1.62 cm, in the middle: 1.7 cm, at string nock: 1.82 cm. Ear length: 9.5 cm, ear angle: 51˚. Grip angle: 156˚, limb length with kasan gözü: 43 cm, limb width at widest point: 3.46 cm, limb thickness in the middle of bending part: 1.18 cm, brace height: 17.5 cm, with shorter string: 21.5 cm. Weight: 488 g, grip size: 2.62×3.55 cm.
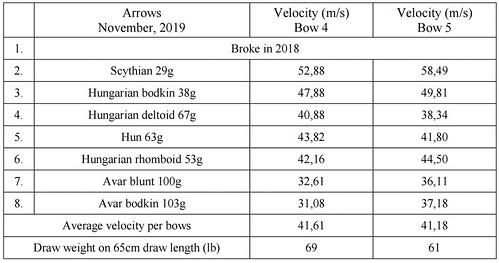
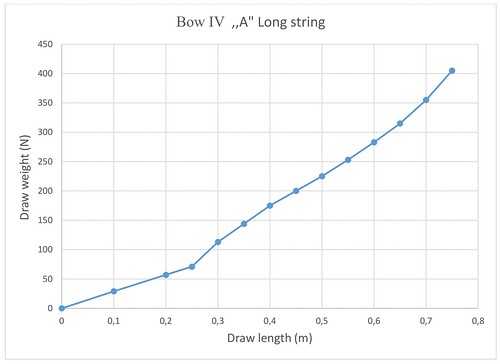
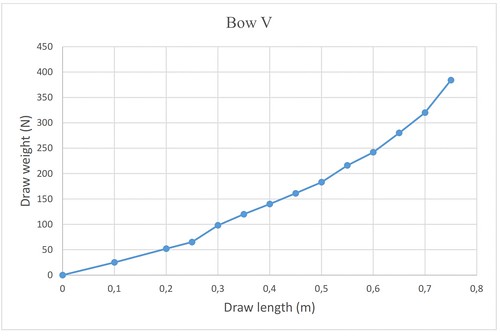
While testing Bow IV and Bow V, I didn’t have a shooting rack, so the shots were executed by hand. We recorded the force-draw values of Bow IV and Bow V in advance. Then velocity measurements took place with all the arrows using a chronograph placed 2 m from the launching spot just like in 2018. Next, the flight shots were carried out. (Data in Appendix 5) Considering the average initial velocity of all arrows, the values of Bow IV and Bow V revealed slight differences from Bow II and Bow III, however, inconsistencies have been seen due to hand shots. While shooting by hand, despite all efforts, the archer, mainly in the case of eastern shooting techniques, makes an extra movement with its bow hand towards the target (hatra), which can increase the initial velocity of the arrow. Furthermore, the twisted grip / grip torque reduces the oscillation of the flying arrow that also influences the velocity favourably.[17]
Bow IV had a too long string to its ear angle, the bow unstrung itself – threw the string out – during shooting so we again recorded the force-draw values with a shorter string. The force-draw curve obtained with the two different strings can be seen in the illustration.) For curiosity, we shot some arrows without a thumb-ring as well based on the previous hypothesis that the initial velocity of these is lower[18], but our data didn’t confirm it. This question must be dealt with in another experiment, and also another one too: how much the achievement of a composite bow strung for a longer time changes compared to a freshly strung one. In other words, the internal friction (hysteresis) of the bow should also be tested (Pictures 31-33).

Picture 31

Picture 32

Picture 33

Arrow tests

Data of the arrows tested during the experiment

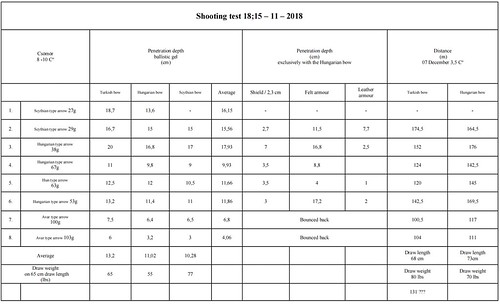
For the sake of homogeneity, I bought and glued turkey feathers on all arrows. At this phase of the experiment, I tried to decipher and classify the battlefield efficacy of the different arrows. The first step was to measure their initial velocity, then the depth of their penetration in various mediums and last but not least, flight shooting with them. Measurements of penetration took place mainly on measurable materials (ballistic gel, 2.3 cm thick pine boards), finally, for curiosity, we shot on a lamellar leather and massive felt armour.

Some sentences about the physics of the arrows

The penetration power and the maximum range of an arrow are influenced by many factors. Gravitational force is composed of gravity and the centrifugal force due to the rotation of Earth. Gravitational force and the arrow mass create gravitational acceleration together. Beside gravitational force and the arrow mass, the drag and the aerodynamic buoyancy also influence the trajectory of the arrow. The drag is inverse to the direction of the flight, meanwhile the aerodynamic buoyancy is perpendicular.
The drag force is influenced by the arrow velocity in the medium. The size and shape of the arrow tip are also crucial factors as they determine if the airflow alongside the flying arrow is laminar or turbulent. If it is mostly turbulent, the degree of the drag coefficient increases. The shape of the wooden shaft and the width of the nock (relative to the diameter of the shaft) also affect the character of the airflow and the drag, just like the height, number, placement of the fletching and its distance from the nock.
The distance between the centre of gravity and geometric centre of the arrow determines the aerodynamic stability. If we increase the weight of the arrow tip so as to reach a deeper penetration, the arrow velocity decreases. However, if we decrease the height of the fletching (surface) at the same time, we can win back some of the lost velocity. The stability of the flying arrow is guaranteed by a centre of gravity upfront, i.e. forward of the geometrical centre, and the arrow’s axial rotation which is provided by fletching. The rotational energy is fed by the kinetic energy of the arrow which results in further velocity loss. Another influential factor is the oscillation of the arrow after release which causes the phenomenon known as the “archer’s paradox”. The degree of oscillation is determined by the poundage of the bow and the flexibility of the shaft (called SPINE rate). The degree of the oscillation is ‘ideal’ when the poundage of the bow and the arrow spine are proportional to each other. (It wasn’t always so during the experiment.)[19]
The arrow velocity, as I mentioned above, was measured by a chronograph 2 metres from the spot of shooting. Due to the oscillation, the chronograph was not always able to measure the arrow, because at the spot of measurement the arrow flew traverse.[20]
The spine value[21] of some arrows, such as Arrow 1 and Arrow 2 which were made of lathe-turned linden and their diameter was smaller (8.1 mm), was not suitable for the heavier bows. Furthermore, in the case of the arrows with heavier tips, the ratio between the weight of the tip and the shaft was not ideal.
As for the efficacy of the arrows, the Scythian type bronze tipped (Arrow 1 and 2) arrows performed better than expected. Because of their smallest weight, their initial velocity was the highest. The Hungarian bodkin-tipped arrow (Arrow 3) also showed reasonable velocity values, while the Avar arrows with three-edged heads (Arrow 7 and 8) performed very badly. In the case of Arrow 1 and Arrow 2 the shaft had to be carved very thin at the root of the tip, which was threatened with the risk of breaking, but despite it, they didn’t break when penetrated the ballistic gel, the leather armour or when hitting the ground. Only the wooden shield was too tough for them so they broke into it. The heavy Avar tips (7 and 8) penetrated the ballistic gel maximum up to the head-shaft connection, but they bounced back from the armours, and they performed awfully during flight shooting too. The efficacy of these arrows was also examined by Holger Riesch and he had the same result[22]. (Pictures 34-38)

Picture 34

Picture 35

Picture 36

Picture 37

Picture 38

As for penetration depth and distances, Arrow 3 achieved the best. Historically it would be a mistake to compare the Scythian bronze headed arrows with the latter iron-headed arrows, however, comparing the Hungarian bodkin head (3) and the short-edged deltoid (4) or the rhomboid head (6) raises some questions.
If the bodkin arrowhead penetrates the deepest and flies the further in flight shooting than the arrows with heavier heads in the same age, what can be the reason for less archaeological findings from the 10th century than those of the deltoids and rhomboids? It is really less common overall, but in some graves bodkin heads dominate. For example, in the Kiszombor-B. 310 grave beside a flat, short-edged deltoid tip and a long-edged deltoid tip, 9 bodkin heads were found. In the Deszk-D. 65 grave, next to a leaf-shaped and an enormous swallow-tail-shaped tip, 5 bodkin heads were found, in grave 6 in Tuzsér 5 bodkin heads were found[23]. If we consider the economical aspect, 18 kg of iron is needed for 2,000 arrows with 9 g bodkin heads, but 52kg is needed for 26 g deltoid heads. Even if an economy has a huge siderurgy and an inexhaustive iron-stone deposit, it matters whether they “throw” 18 or 52 kg of iron to the enemy. In other words, if the enemy can be defeated with 18 kg of iron, why is it necessary to waste 34 kg more iron? And now I am talking about only 2,000 arrows.
The solution probably can be found in the wounding ability of the different arrow tips. The relatively blunt edged tip with square cross section may harm the living tissue less than the flat tip which is sharp on both edges. In 1388 AD, Gaston de Foix writes in his hunting book that the long-edged arrow tips are efficient because the long edge causes such a pain to the animal that it cannot escape even if the wound is not lethal[24]. Can it be the reason in the case of humans too? In Toxophilus by Roger Ascham in the 16th century, the thin, flat edged arrow tips are also considered to be painful, on the other hand, he supports the square heads because they penetrate the body deeply, they are easy to pull out so it quickens the death of the wounded person. Ascham considers the bodkin head to be a war tip, while Sebestyén Cs. thinks it is definitely a hunting tip[25]. During his test shooting on a swine corpse, Hubert Sudhues observed that the edgeless square head tented the punctured intestines, while the flat sharp head cut it immediately and the content of the intestines flew out[26]. It is obvious that the use of certain arrowheads are determined by the enemy’s armour or lack of armour. [27]In the 10th century findings the short-edged, deltoid head is the most common (which is generally used in the Eurasian Steppe, so it is well-tried) and very efficient against the enemy without chainmail or other armour. Furthermore, the bodkin head penetrates the chainmail at least up to the head-shaft connection to the root, which was proved with shooting tests earlier (Pictures 39-40)[28].
Pictures: Zoltán Füspök

Picture 39

Picture 40

If the enemy is not armoured, or the mounted archers with bow and arrows avoided meeting the armoured enemy, instead of the bodkin heads, using the flat, sharp-edged tips were more sensible.
Testing the arrowheads from Avar findings raises similar questions. Why does an army use arrows with 54-56 g tips whose penetrating ability is bad and cannot be shot far if they certainly use 9-10 g tips too? 112 kg of iron is needed in the case of 2,000 arrows with 56 g tips opposite the 18 kg of iron for 9 g tips; the difference is outstanding. What makes an army use such an amount of iron? Obviously the armoured enemy, so we can make the logical deduction that this type of arrow tip can harm the armoured enemy to some extent. We know partially lamellar (Kunszentmárton, Tiszavasvári, Hajdúdorog)[29] and fully lamellar metal armours from Avar findings (Derecske-Bikás dűlő)[30]. This armour type was known not only by the Avar heavy cavalry but also the Franks and Byzantines who fought against them. Findings and depictions witness that this armour type was widely known in the ancient times too[31]. After earlier experiments[32], it was obvious for me that neither the three-edged nor the flat tips penetrate neither the lamellar armour nor the chainmail. But if the enemy’s armour cannot be penetrated with the given tools, the man behind the armour should be put out of action somehow. (In November, 2019, after determining the use-value of Bow IV and V, we shot on 25×25 cm bradded wire armour piece with Bow IV and Arrow 8.)
I tied up the chainmail piece on a cylindrical straw bale, whose substance was not too different from the human body as for density. I didn’t put it too tight (so it was not on a board) because the tightness of the chainmail and the “background” behind it influence the penetration on the chain-links[33]. We shot with Bow IV with 75 lb draw weight from 12 metres. The result justified my hypothesis: the chain-links were harmed minimally but the arrow didn’t penetrate the chainmail piece[34].
I assume that even if the arrow, known from the Avar findings with a huge tip, doesn’t penetrate the armour, hits the man so badly that his bones would be broken or he would simply be thrown off the horse. I wanted to confirm or disconfirm this hypothesis during the third experiment of the shooting test on 22nd March, 2020, when with Arrow VII which we tested earlier (100 g, 56 g concave tip) we shot at a 31×33 cm lamellar metal armour which was made of 1 mm thick flattened steel plates and contained almost 100 pieces of 8×3 cm “roof-tile”-shaped plates (maker: Ákos Sándor Wilhelm)[35]. We also shot on pig-sided hidden behind the armour, with Bow II which is known from the earlier phase of the experiment. I didn’t put any fabric or gambeson between the armour and the pig-sided, I wrapped the pig-sided with nylon, I put a sack puppet behind it, which was the height of a man and as tough as a human chest. The target was placed 12 m distance from the place of release, the height of release was 2.5 m so as to have the suitable angle of incidence. After the shots, I thoroughly examined the ribs of the pig-sided, the bones remained completely intact except for the rib (os costale) which was exposed from under the armour, the arrow broke it (Pictures 41-46).

Picture 41

Picture 42

Picture 43

Picture 44

Picture 45

Picture 46

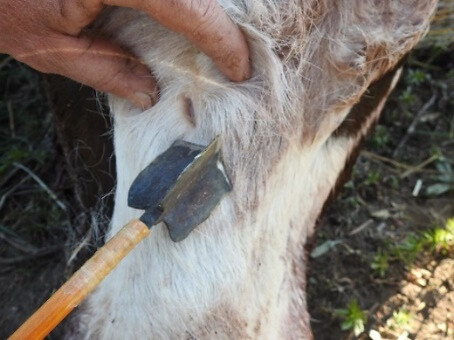
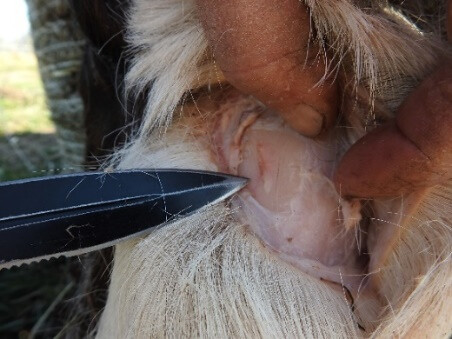
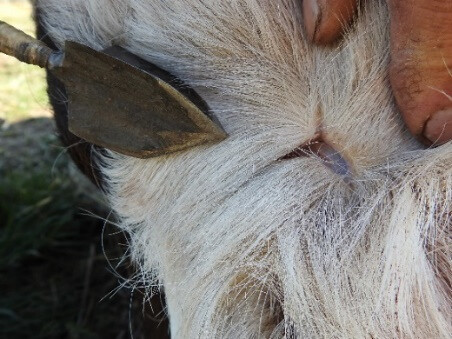
After shooting on the armoured puppet, I put on a double wadded linen gambeson, then a hard felt armour, lastly, I tied the lamellar metal armour piece on my chest. After the necessary safety measurements, my assistant shot at my chest with Bow II and Arrow VII from 12 m distance. The hit of the arrow didn’t make me faint or lose my balance and in my opinion, the hit wouldn’t have knocked down any man in the battle. After all these, I assume that the tested arrows were not used to knock down the armoured enemy, but maybe to bruise the parts of the horses exposed from under the horse armour[36]. As the raison d’etre of the blunt Avar arrowheads is still not unravelled (János Kalmár considers them as hunting or fire tips)[37], and I couldn’t obtain horse body parts, on 3rd April, 2020, I shot at the head and front legs of a decapitated five-year-old cow with Bow II from 12 m distance. Arrow 7 was damaged so badly during shooting on the armour that I had to make two new arrows. I had only lathe-turned 10 mm diameter pine shafts, on which I put a 48 g and a 62 g good quality but not precisely made, blunt-tipped (not concave) forged iron head.
I still had Arrow 8 used earlier, and I also used its replica (8/b) which had almost the same size and weight (Picture 47).

Picture 47

From the experiences of Hubert Sudhues’s experiments I thought that wounds in the size of the arrowhead are created on the skin (which is not always so in the case of certain arrowhead shapes). Furthermore, in the case of the hits caused by blunt arrowheads, erratic tissue damage appears under the skin. In the case of bones, the shape of the arrowhead also determines the shape of the injury. Moreover, the power, angle of the hit and the toughness of the bone determine the degree of deformation. The steel heads may be broken while hitting bones, and the softer metal or bronze heads may bend[38]. We obtained the following experiences (Pictures 48-59):

Picture 48

Picture 49

Picture 50

Picture 51

Picture 52

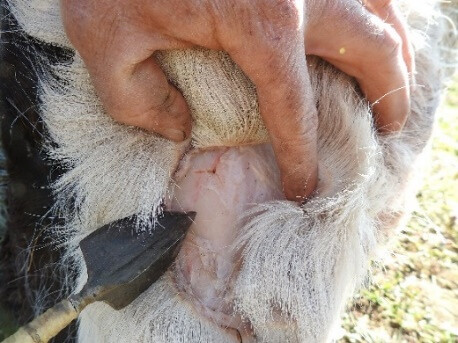
Picture 53

Picture 54

Picture 55

Picture 56

Picture 57

Picture 58

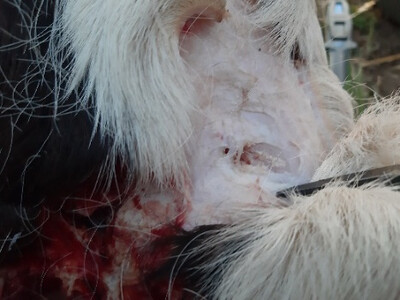
Picture 59

1st shot with Arrow 8: it hit the forehead (os frontale), and despite the fact that the tip is not blunt but sharp it bounced off after cutting the skin tissue, however, it left a hole on the bone surface with resembling its shape.
2nd shot with the 62 g blunt tip: it hit the nose bone (os nasale), after cutting the skin tissue it made a 2 cm-long crack on the bone.
3rd shot with the 48 g blunt tip: it hit the nose bone, after cutting the skin tissue it bounced off and didn’t cause any indiscernible lesion.
4th shot with the 48 g tip: it cut the skin tissue of the eyebrow and “skipped” aside.
5th shot with the 48 g tip: it directed the leg. The arrow penetrated the horn of the two nails, got nipped between the nails, and due to the oscillation the arrow shaft broke close to the tip.
6th shot with the 62 g tip: it cut the skin tissue of the left eyebrow and “skipped” aside.
7th shot with Arrow 8: it directed the leg. It hit the bones of the fetlock joint (ossa sesamoidea proximalia) and glanced off and broke one of the cartilages of the joint.
8th shot with Arrow 8: it hit the forehead.
9th shot with Arrow 8: it hit the side of the nose bone (os nasale), the tip penetrated the bone after cutting the skin and muscle tissues.
10th shot with Arrow 8: it cut the toe bending tendons of the leg on the part which was not covered with skin.
11th shot with the 12 g flat iron tip: on the forehead (os frontale): the arrow penetrated the bone to its two-third after cutting the skin tissue. Up to this point, this tip penetrated the forehead the deepest.
12th shot with Arrow 3 (Hungarian bodkin head): on the nose bone (os nasale). The arrow cut the skin tissue and penetrated the nose bone 8 cm deep.
13th shot with Arrow 3: on the forehead (os frontale): the arrow penetrated the bone till the length of the tip (3 cm) after cutting the skin tissue. When we tried to pull it out, the glue did not stand and the tip came out of the wooden shaft and remained in the bone.

New, minimally oxidized, big-sized arrowheads were found during the excavation of the cemetery from the Avar era in Babarc.[39] This recent information can change our hypotheses about the weight of arrowheads.

Conclusions

The heavy Avar arrowheads haven’t caused more serious wounds on the cattle skull than the lighter, flat rhomboid shaped or square cross sectioned bodkin heads. Therefore, their use still seems illogical due to the need of enormous iron for them. Not to mention that with the much smaller and simpler heads the bones of the skull and legs can be harmed in the same way. As it is forbidden to shoot on a living animal, it cannot be identified how it influences a saddle-horse’s work, activity and stoppability if it is shot with a 60 g heavy, blunt, three-bladed head or with a smaller one. If we consider that a horse can be disturbed even with a branch thrown towards it, it is imaginable what confusion a rain of arrows with huge arrowheads could cause in the enemy’s battle formation. However, we cannot ignore Holger Riesch’s idea which states that the Avar arrowhead inventory wasn’t used in the Meroving era Frank archery although they existed in the same age. The reason for it can be either they questioned the efficiency of the huge arrowheads, or they had problems in producing such types of arrowheads[40].
The process of making bows, arrows and even arrowheads is determined by generative creativity. According to this, a given society decides how to make all the tools they use, and the makers “dare” to deviate only slightly[41]. Possibly, the Avars took the heritage of making and using the heavy, three-bladed arrowheads from Central Asia. During times, the arrowheads gradually got bigger and bigger, just like the arrow limbs got unreasonably wider and wider by the late Avar era. Based on simple observations without using any device, the penetration power of an arrow can be increased by increasing the weight of the arrowheads. The acceleration due to gravity starts increasing which is the result of increased gravitational force. Simultaneously, after reaching the top of the parabola of its trajectory, the kinetic energy of the arrow starts increasing again. However, the full amount of kinetic energy at the moment of release cannot be gained back by increasing the weight of the arrowhead[42], so increasing the arrowheads becomes a burthen after a certain point. I assume that the tradition of making and using the enormous Avar arrowheads became a tradition literally as there was no way to observe the arrows with any devices. Furthermore, the all-time enemy was probably frightened by the huge arrowheads flying towards them, and at the moment of infall they didn’t think about the reasons why the Avars wasted such a huge amount of iron if they were able to destroy on the same or even a higher level by using much smaller arrowheads.
I hope our writing, with all the imperfection and probable seeking ways of our experiments, will grab those readers’ attention who are seriously interested in traditional archery. We hope they will continue researching on the given base taking no little pains over time and effort to help us get to know the former Steppe people’s archery thoroughly (Appendix 1).

This article was published in the 4th issue of 133rd volume of ‘Hadtörténeti Közlemények’ magazine in December, 2020 (p 953-997).

1. Settlement era: in 895-896 BC the Hungarians settled down in the Carpathian basin; according to the latest theory, the whole process took place gradually, from about 860 till 902
2. Szőllősy 1995a.
3. Riesch 2009, p 62
4. Prestressed: the bending of the bow towards the target in unstrung state is called reflex and provides a pre-tension when the bow is strung and not drawn yet compared to bows with straight limbs in unstrung state (the translator’s note)
5. A bow is a string-follower when its limbs bend towards the archer due to frequent use or overuse.
6. Riesch 2009, p 64
7. Deflex: the part of the bow which is counteractive to the reflex and bends towards the archer.
8. Brace height: the distance between the grip and the string on a strung bow
9. A rekonstrukciók, rekonstruálhatóság problémájára: Lásd: Szőllősy 2004. p 57; Igaz 2009; Bíró 2013 p 214-217
10. Kasan gözü: part of the reflex of the Turkish bow, between the working limb and the ear, or more accurately kasan which is a ridge whose horizontal cross-section has almost a triangle shape.
11. Varga 2013, p 71-73
12. Szőllősy 1995b. p 39-40
13. Godehardt 2009, p 46
14. Riesch 1999
15. Szőllősy 1995a, p 4
16. If a bow is left strung in long periods of time it undergoes a plastic deformation and doesn’t take its original shape when unstrung. This permanent deformation towards the direction of stringing is called “string follow”. – Translator’s note
17. Özveri 2018. p 175-183
18. Özveri 2018. p 126-128
19. Hegedűs 2013. p 7-10
20. Translator’s note: The two sensors of a chronograph spot a moving object in move and calculates the velocity by using the time that the object travels between these two sensors. A severely oscillating arrow’s front and rear ends may not be captured precisely enough to make an accurate calculation of speed.
21. Spine value: the measurement unit for expressing the flexibility of the arrow shaft. GNAS (British) AMO (American) measurement. Gábor Szőllősy 1995b. p 16
22. Riesch 2002, p 58-59
23. Sebestyén Cs. 1932, p 199-200
24. Riesch 2002, p 60
25. Riesch 2002, p 61; Sebestyén Cs. p 200
26. Sudhues 2004, p 104
27. Töll 2009 p 53
28. M.T.Í.T. shooting test, October 2018: Adács 2018; Igaz 2010, p 287
29. Csallány 1960, p 17
30. Exhibiton in Déri Museum, Debrecen: The Rider of the Kaghan, 2 October – 31 December, 2019 (Derecske, Bikás dűlő, full Avar lamellar armour, archaeologist: Tamara Hága)
31. Pintér-Nagy 2014, p 95-97; Riesch 2017, p 185-193
32. M.T.Í.T. shooting test October 2018, Adács 2018; Riesch 2017, p 185-193
33. Töll 2009, p 50-53
34. Riesch 2002, p 58-61
35. Csallány 1972, p 11-12
36. Szádeczky-Kardoss 1988, p 80
37. Kalmár 1944-1945, p 284-286
38. Sudhues 2004, p 114-118
39. The author’s additional notes in 2023
40. Riesch 2002, p 63
41. Szőllősy 1995b, p 80
42. Szőllősy 1995b p 14, Szőllősy (based on Hickman) shows a bow efficacy curve from which it is clear that by increasing the weight of the arrowhead, 80% of the initial kinetic energy can be gained back.